All exercise S.Qs of Chapter#5: Relavastic Quantum Mechanics of Quantum Mechanics-II. We have arranged all S.Qs for BS/MSc Physics students.
Q.1 Differentiate between relativistic and non-relativistic quantum mechanics.
Answer: The part of quantum mechanics based on the Schrodinger wave equation describes the particles moving with very low velocities comparing with velocity of light is known as Non-relativistic Quantum Mechanics.
Moreover, old Schrodinger wave theory fails to explain the spin of a particle. The part of quantum mechanics based on the Schrodinger wave equation which describes the motion of a particle that has a speed approaching the speed of light is known as Relativistic Quantum Mechanics.
Q.2 Why K.G. Eq. describe the particles with zero spin?
Answer: Klein-Gordon equation i.e.
$$\left(\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t}\right)\psi_{(r,t)}=\frac{m_\circ^2c^2}{\hbar^2}\ \psi_{(r,t)}$$
is an equation for one component only, the single component is ψ itself. For a spin (2S + 1), there are values. For value. Thus K.G equation is for a particle whose . So this equation does not represent a particle whose spin is 1/2
Q.3 Define two difficulties of K. G. Eq.
Answer:
1st Difficulty: The probability density for a particle is not possible, we know that,
$$\rho_r=\frac{i\hbar}{2m_\circ c^2}\left[\psi^\ast\frac{\partial}{\partial t}\psi-\psi\frac{\partial}{\partial t}\psi^\ast\right]$$
As $\rho_r$ denotes the probability and it must be non-negative i.e. positive. This is the fundamental difficulty of accepting Klein-Gordon equation as a relativistic equation in quantum mechanics.
2nd Difficulty: Another problem with 1/2 equation is that, it does not represent a particle with spin 1/2 (fermions). This is because, Klein-Gordon equation i.e.
$$\left(\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t}\right)\psi_{(r,t)}=\frac{m_\circ^2c^2}{\hbar^2}\ \psi_{(r,t)}$$
is an equation for one component only, the single component is itself. For a spin S, there are (2S+1) values. For $S=\ 0\ ;\ \ \left(m_s\ =\ 2S\ +\ 1\right)={2\ (0)\ +\ 1}\ =\ 1$ value. Thus K.G equation is for a particle whose S=0. So this equation does not represent a particle whose spin is 1/2. These difficulties were removed by Dirac 1st order differential equation.
Q.4 Differentiate between K. G. Eq. and Dirac Eq.
Answer: Special theory of relativity says that equation must be Lorentz invariant. Work on relativistic quantum mechanics was firstly formulated by Schrodinger (1926), Klein (1927) and Gordon (1926). They suggested Klein-Gordon equation in 1927 which was a 2nd order wave equation rather than Schrodinger equation. The Klein-Gordon equation was initially dismissed, since it led to negative probability densities. In 1928, the Dirac gave another equation that was related to fermions. The Dirac equation, like the Klein-Gordon equation, possesses the solutions with negative energy which cannot be explained by wave mechanics. To prevent transition of an electron into negative energy states in 1930, Dirac postulated that the states of negative energy should all be occupied which contain particles with opposite charge (anti-particles). This necessarily leads to a many particle theory, or to a quantum field theory. In 1934, W. Pauli and V. Weiskoof reinterpreted the K.G. equation as the basis of a Quantum Field Theory.
Q.5 Define Lorentz invariant transformation.
Answer: The Schrodinger wave equation for a free particle (V=0) in non-relativistic case in the coordinates representation is given by
$$\hat{H}\psi=E\ \psi$$
$$\left[\frac{-\hbar^2}{2m}\nabla^2+V\right]\psi=i\hbar\frac{\partial}{\partial t}\psi\ \ \$$
$$\frac{-\hbar^2}{2m}\nabla^2\psi=i\hbar\frac{\partial}{\partial t}\psi\$$
$$i\hbar\frac{\partial}{\partial t}\psi=\frac{-\hbar^2}{2m}\nabla^2\psi$$
The different orders of the time and the space derivatives shows that above equation is not Lorentz covariant (an equation that changes its structure under a transition from one inertial system to another)
Q.6 Write down the Dirac spinors.
Answer: The Dirac spinor is
$$\psi\left(r,t\right)=\left(\begin{matrix}\psi_1(r,t) \\ \psi_2(r,t) \\ \begin{matrix} \psi_3(r,t) \\ \psi_4(r,t) \end{matrix} \end{matrix} \right)$$
Q.7 Define Pauli spin matrices.
Answer: The Pauli spin matrices are,
$\sigma_1=\left(\begin{matrix}0&1 \\ 1&0 \\\end{matrix}\right)_{2\times2}$, $\sigma_2=\left(\begin{matrix}0&-i \\ -i&0 \\\end{matrix}\right)_{2\times2}$ , $\sigma_3=\left(\begin{matrix}1&0 \\ 0&-1 \\\end{matrix}\right)_{2\times2}$
Q.8 Why Dirac equation explain spin 1/2 particles?
Answer: In 1928, P.A.M Dirac discovered the relativistic wave equation with a definite positive probability density. Dirac equation explains the particles of spin 1/2 e.g. electron. In non-relativistic quantum theory, particles of spin 1/2 are described by the two spin states
$$\left(S_z=m_sh\ \ \ \ ;\ \ \ m_s=\pm\frac{1}{2}\right)$$
In relativistic theory, it is also considering the fact of anti-particle having the same mass and spin but of opposite charge, we need a four component wave function. This was the achievement of Dirac equation that able to predict the existence of positron.
Q.9 Explain negative energy states.
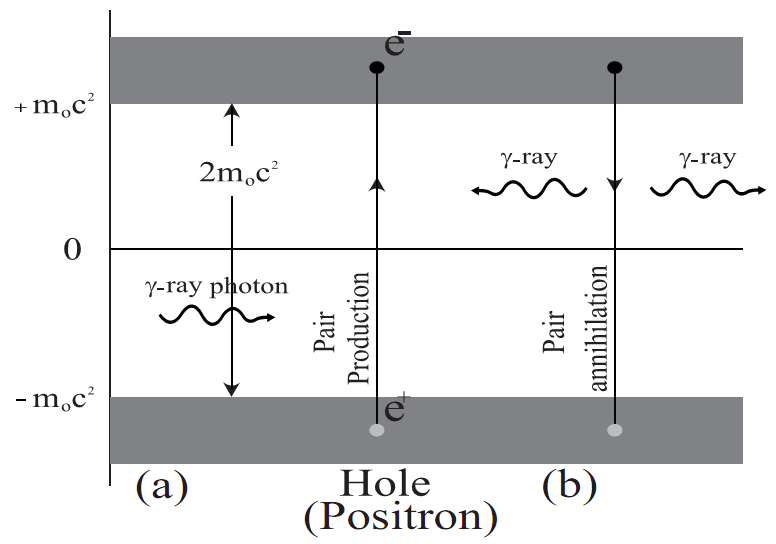
Answer: Dirac equation gives four independent solutions. Two for +ve energy and two for -ve energy states. The -ve energy states can not be ignored on the basis that they are unphysical. Since, all the four solutions together form a complete set. i.e. $\sum_{i=1}^{4}{\psi_i\psi_i^\ast}=I$. This reflects that, electron in the +ve energy states can make transition to -ve energy states at the estimated rate of ${10}^{-8}$ sec. This is disastrous and no stable atom is possible if such transitions are allowed to -ve energy states. Dirac gives a bold suggestion in the form of Hole Theory, to overcome this difficulty. According to this theory -ve energy states are assumed to be completely filled by electrons. The Dirac vacuum is one in which all -ve energy states are filled and all -ve energy states are empty. Thus, Pauli Exclusion Principle does not allow any transitions of -ve energy electrons. The -ve energy electrons can absorb radiation of energy $>2m_\circ c^2$ and jump into +ve energy states. In doing so, a “hole” is left in the Fermi sea. Thus Dirac equation together with hole theory predicts the existence of positron. In 1932, Anderson discovered the positron experimentally and got Nobel prize in 1936.
Q.10 What are the potential applications of positron?
Answer: Positron has many applications such as large beam life time positron emission tomography (PET), positron in synchrotron light source, positron annihilation life time spectroscopy.

